介绍

可重构计算-技术路径

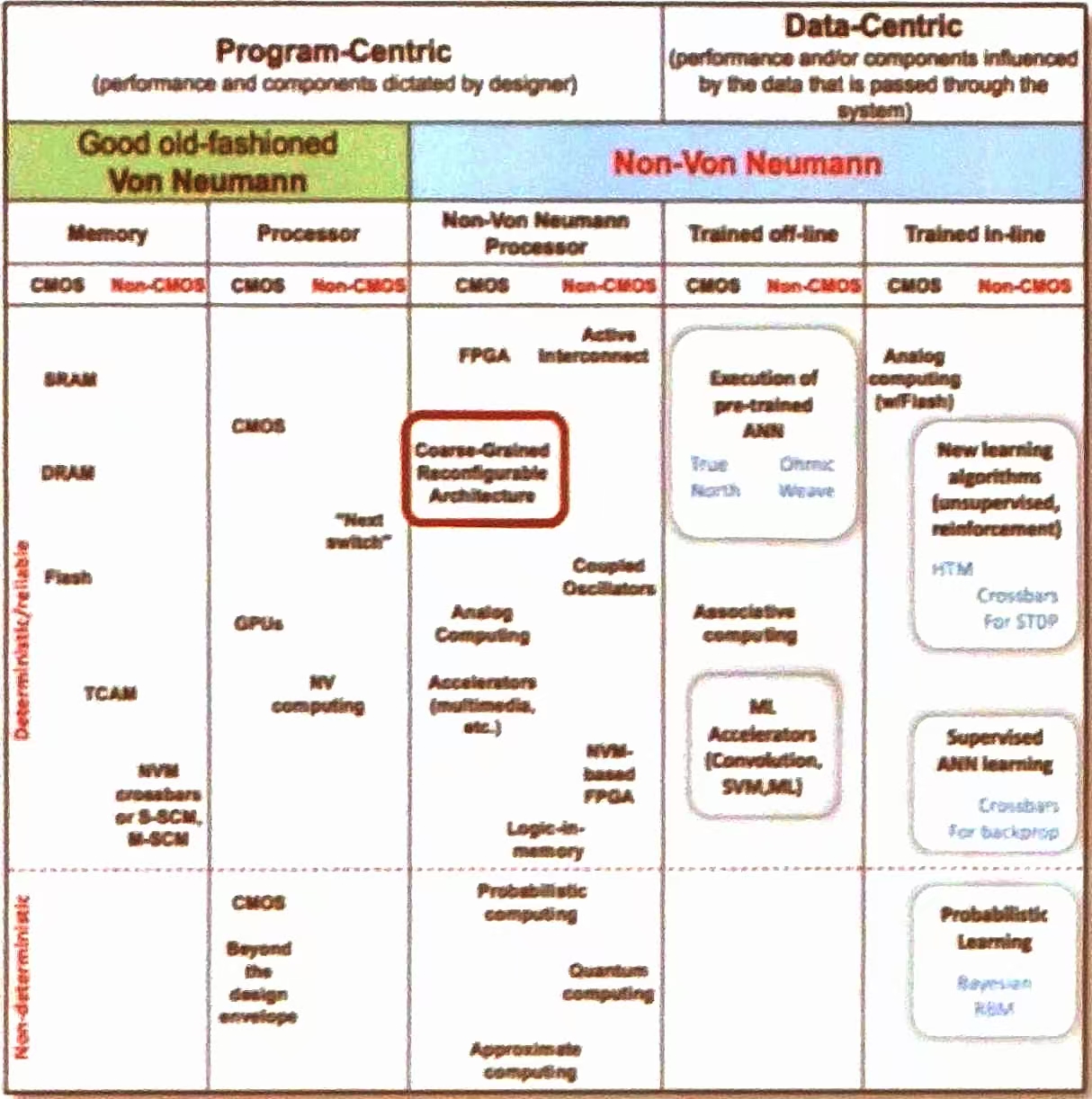
alt text
主要将其计算架构分为两大类：

  • 程序中心型（Program-Centric）：性能和组件由设计者决定。
  • 数据中心型（Data-Centric）：性能和/或组件受通过系统的数据影响。

程序中心型细分

传统冯·诺依曼架构（Good old-fashioned Von Neumann）

  • 存储器（Memory)
    • COMS 技术：SRAM、DRAM、Flash
    • 非 COMS 技术：NVM crossbars or S-SCM, M-SCM
    • 其他：TCAM
  • 处理器（Processor)
    • COMS 技术：GPUs
    • 非 COMS 技术：“Next Switch”
    • 其他：NV computing

非冯·诺依曼架构（Non-Von Neumann）

  • 处理器（Non-Von Neumann Processor）
    • COMS 技术：FPGA、粗粒度可重构架构（Coarse-Grained Reconfigurable Architecture）、模拟计算（Analog Computing）、加速器（Accelerators (multi-die)）
    • 非 COMS 技术：Active interconnect、Coupled oscillators, NVM-based FPGA、量子计算（Quantum computing）(不确定)
    • 其他：逻辑内存(Logic in Memory)、概率统计计算 (Probabilistic computing)（不确定）、近似计算（Approximate computing）（不确定）

数据中心型细分

离线训练（Trained off-line)

  • 执行预训练ANN：如True North、Omic Weave等。
  • 关联计算
  • ML加速器（卷积、SVM、ML）等。

在线训练（Trained in-line）

  • 新学习算法：如无监督学习、强化学习等。
  • 监督ANN学习：如交叉点用于反向传播等。
  • 概率学习：如贝叶斯RBM等。

可重构计算-实现机制

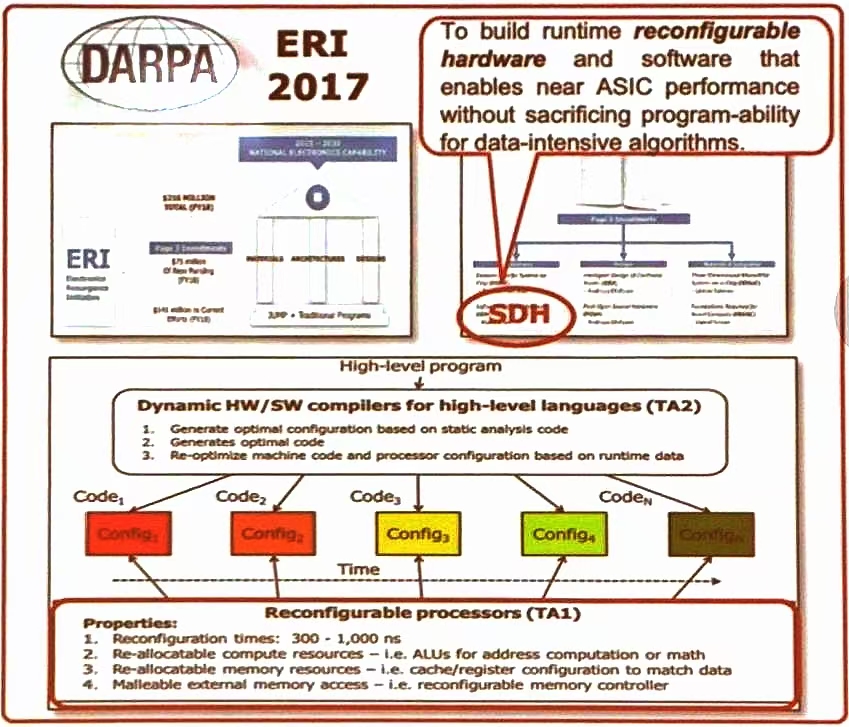
alt text

目标

构建运行时可重构的硬件和软件，使数据密集型算法在保持编程灵活性的同时，达到 ASIC 的性能

  • SDH (Software-Defined-Hardware)，即软件定义硬件，使实现这一目标的核心技术

技术架构

高层抽象程序，即通过动态的硬件/软件编译器（TA 2）生成最优配置和代码

  1. 基于静态分析代码生成最优配置
  2. 生成最优代码
  3. 根据运行时数据重新优化机器代码和处理器配置

可重构的处理器（TA 1）

  1. 重构时间在 300 ns-100 ns
  2. 可重新分配计算资源（如 ALU 用于地址计算或数学运算）
  3. 可重新分配内存资源（如缓存/寄存器配置以匹配数据）
  4. 可塑性外部内存访问（如可重构内存控制器）

高层抽象的程序通过编译器生成多个代码段 (Code_1,Code_2,…,Code_n)每个代码段对应一个特定的配置 (Config_1, Config_2,Config_n)。这些配置随时间变化，以适应不同的运行时需求，体现了系统的动态性和灵活性。

SDH（Software defined Hardware）

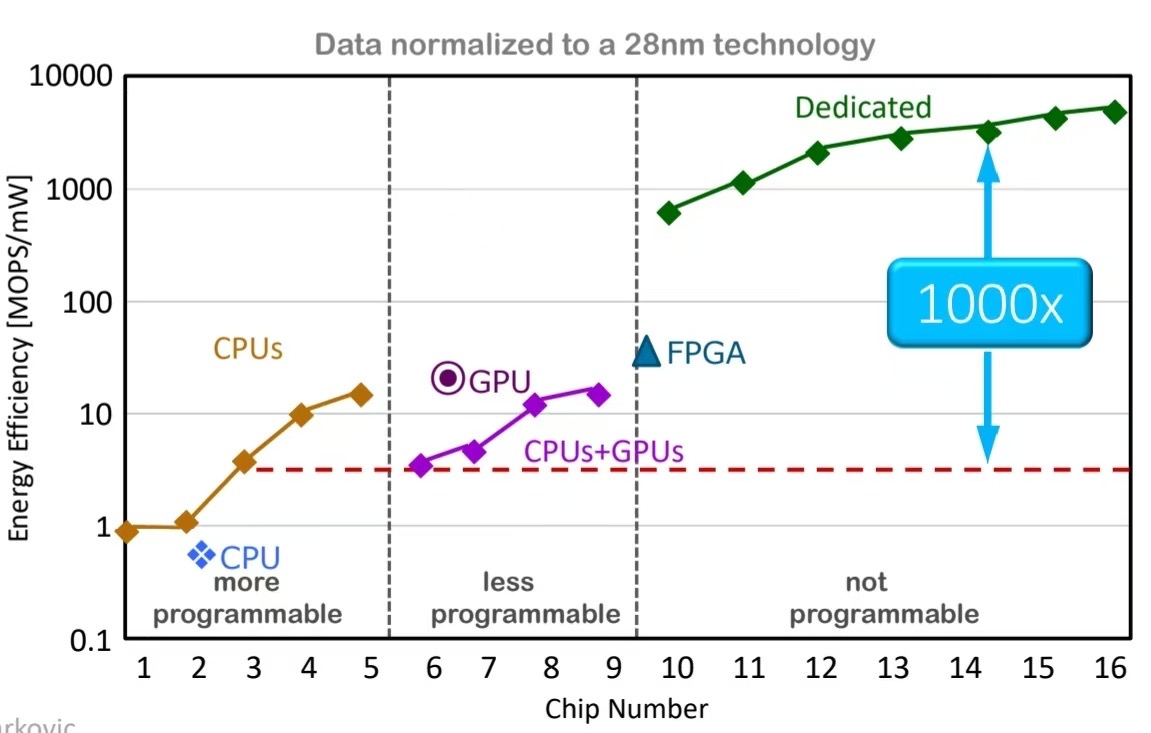
alt text
从图中可以看出不同的计算硬件在能效和编程灵活性之间的权衡关系，强调了 SDH 在这平衡中的重要。

可重构计算：概念

  • 可重构架构：利用可编程资源（处理单元与互连网络）动态配置最适合软件任务的计算架构，实现接近 ASIC 的性能
  • 关键特性：
    • 数据驱动计算，无指令
    • 多重重构层次
    • 时空与串并行调度
    • 兼具灵活性与高能效
  • 计算任务（软件）-> 数据流图-> 数据通路（硬件）

早期应用

可重构计算并非全新概念，其早期应用主要集中在信号处理和通信领域。这些应用场景通常包含算法多样性、实时性约束、数学密集型操作和规整的数据模式等特点。例如，在视频处理中需要运行多种编解码算法，在软件无线电中需要实时处理通信协议，这些都对硬件提出了既要高效又要灵活的要求。因此，像 FIR 滤波器、FFT、OFDM 调制解调等任务，成为了早期验证可重构计算优势的典型负载。

还有一些期可重构处理器在商业应用中的具体实例。例如，三星公司利用可重构处理平台为其8K 超高清电视开发了灵活的视频后处理解决方案，以支持不断演进的新标准。同时，瑞萨电子的 DRP 和 IPFlex 的 DAPDNA-2架构也是可重构技术在通信和信号处理领域成功商业化的代表，它们通过可编程的处理单元阵列和互连网络，为特定领域提供了高效而灵活的计算能力。

为什么要采用可重构计算

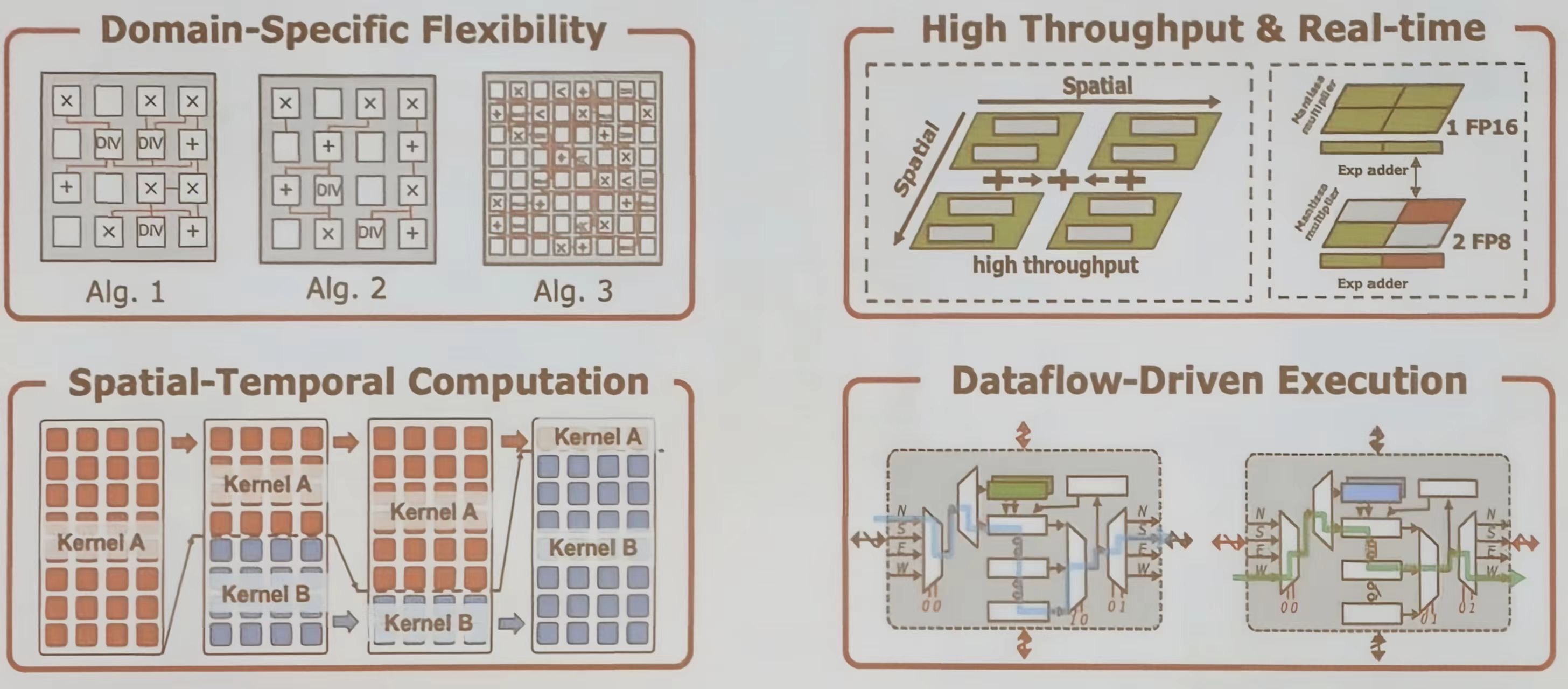
alt text

  • 提供“领域特定的灵活性”，同一个硬件可以高效支持同一应用领域内的多种算法
  • 通过“空间计算”架构，它可以实现高吞吐量和实时处理能力
  • 通过“时空计算”调度，它可以灵活地组合不同计算内核
  • “数据流驱动执行”模型消除了指令开销，提升了效率

挑战

从手势识别、人脸检测到 ChatGPT 等大语言模型，人工智能应用层出不穷。图中曲线清晰地展示了从2012年 AlexNet 开始，深度学习模型在 ImageNet 数据集上的识别准确率急剧提升，同时模型的计算复杂度和参数量也呈爆炸式增长。这预示着到2033年，我们将面临计算需求远超万倍于今天的巨型模型，这对底层计算硬件提出了前所未有的挑战。

与传统的、算法固定且精度单一的信号处理不同，现代神经网络模型展现出高度多样性。一个 Transformer 解码层内部就包含了多种类型的计算（如注意力、全连接），其连接方式（稀疏或全连接）、数据精度 （如 INT 8、FP 16）和拓扑结构都可能不相同。

这种“多样性”是神经网络强大表征能力的来源，但也使得为其设计通用高效硬件变得异常困难。

网络拓扑的多样化是神经网络发展的显著趋势。图中时间轴展示了从早期的简单序列模型（Seq 2 Seq）和卷积网络（AlexNet, VGG，到引入残差连接到 ResNet、自注意力机制 Transformer，再到如今参数庞大的 GPT、PaLM 等大模型。拓扑结构日趋复杂，从单一模态处理发展到多模态融合。这种复杂性要求硬件能够灵活适应从卷积、全连接到注意力等多种计算模式。

硬件要求——灵活的数据流

不同的网络拓扑导致了不同的数据复用模式，进而对硬件数据流提出了灵活性的要求。

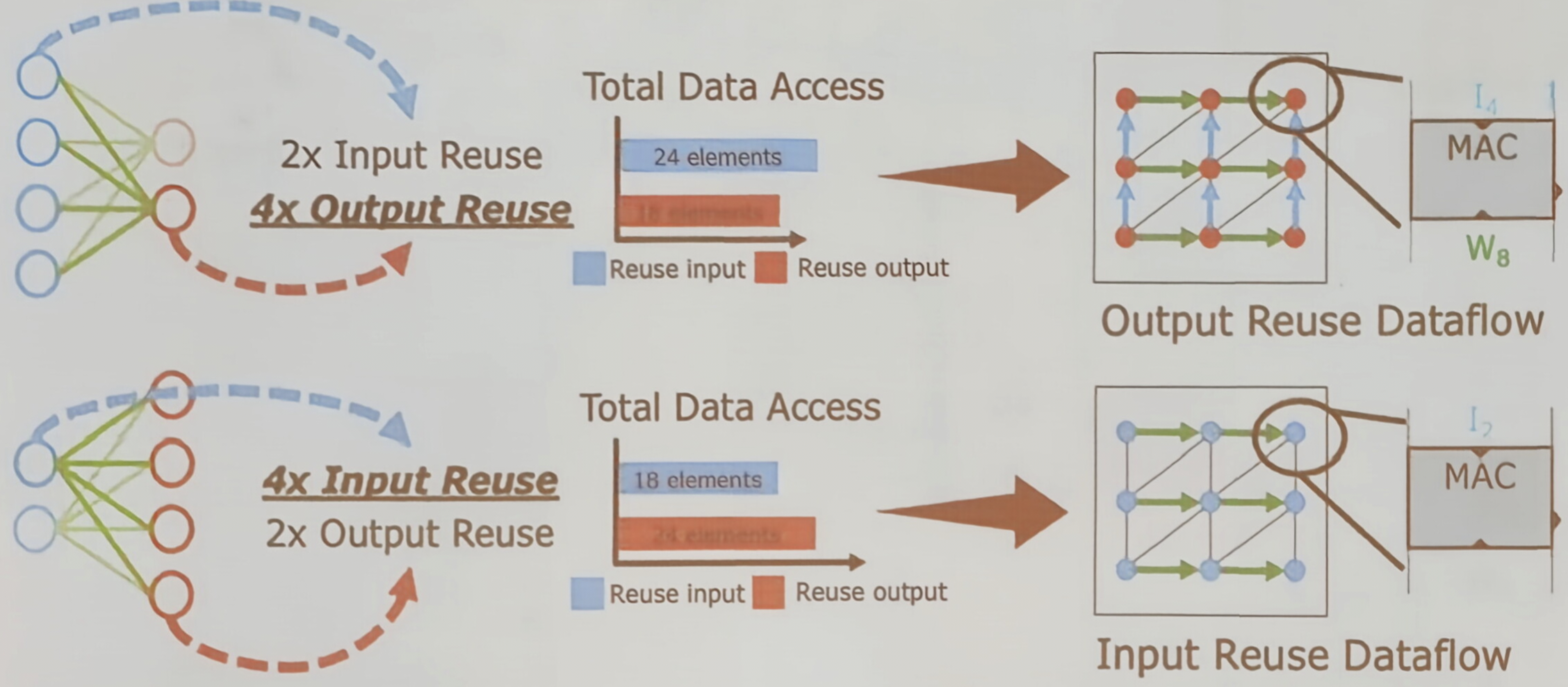
alt text
图示对比了“输出重用”和“输入重用”两种典型数据流。

  • 例如对于某些层，重用输出特征图能最大化减少数据访问；
  • 对于另外一些层，重用输入数据或权重可能更有效

硬件需要能够动态配置数据流，以匹配计算过程中的数据复用特性，从而最小化能耗最高的片外内存访问。

硬件要求——多维稀疏性

稀疏性意味着张量中存在大量零值。如图所示，稀疏可能会出现在输入、权重或输出等多个维度。这些零值在计算中是无效的，如果硬件仍对其进行计算，将造成巨大的资源浪费。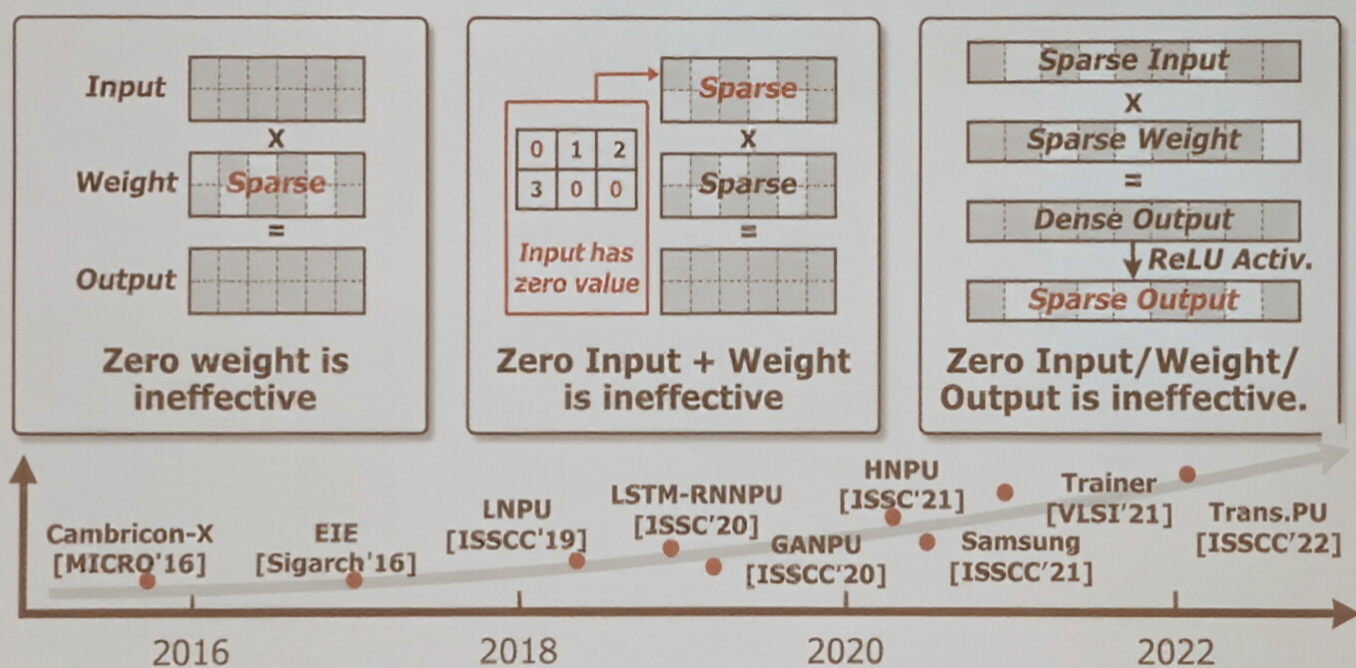
alt text
图中展示了两种处理方式：

  • 对于输入和权重的稀疏，可以进行“逐元素跳过”，只将非零的操作数对送入处理单元队列（PE）进行乘加运算。
  • 对于输出的稀疏，则可以进行“向量级跳过”，避免对整个输出向量的无效计算
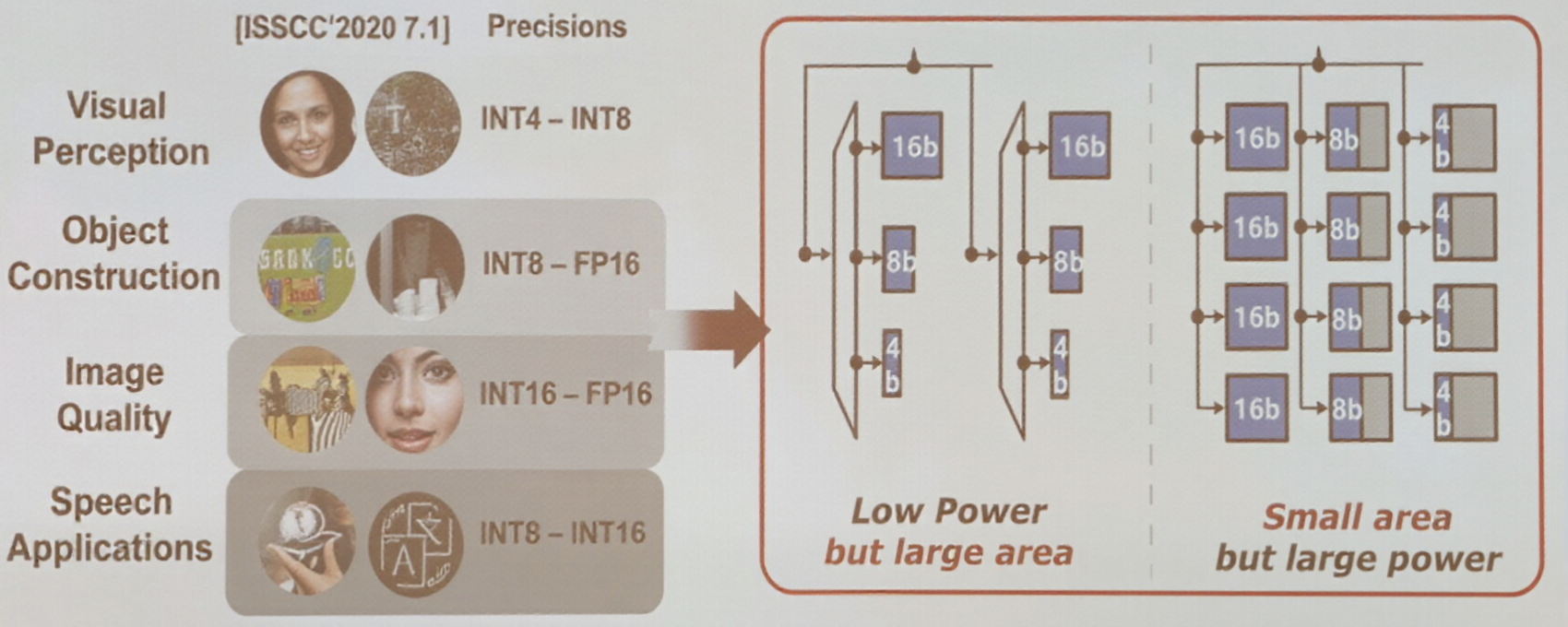
    alt text

硬件要求——精度

数据精度（位宽）的选择是精度、功耗和面积之间的权衡。如图所示，不同的 AI 应用场景对精度的需求个不相同，从低精度的 INT 4 到较高精度 FP 16 等。

  • 采用固定精度处理单元会带来非预期的功耗和面积开销
  • 采用可配置精度的处理单元，则可以根据任务需求动态调整，在保证精度的同时实现最优的能效和面积效率
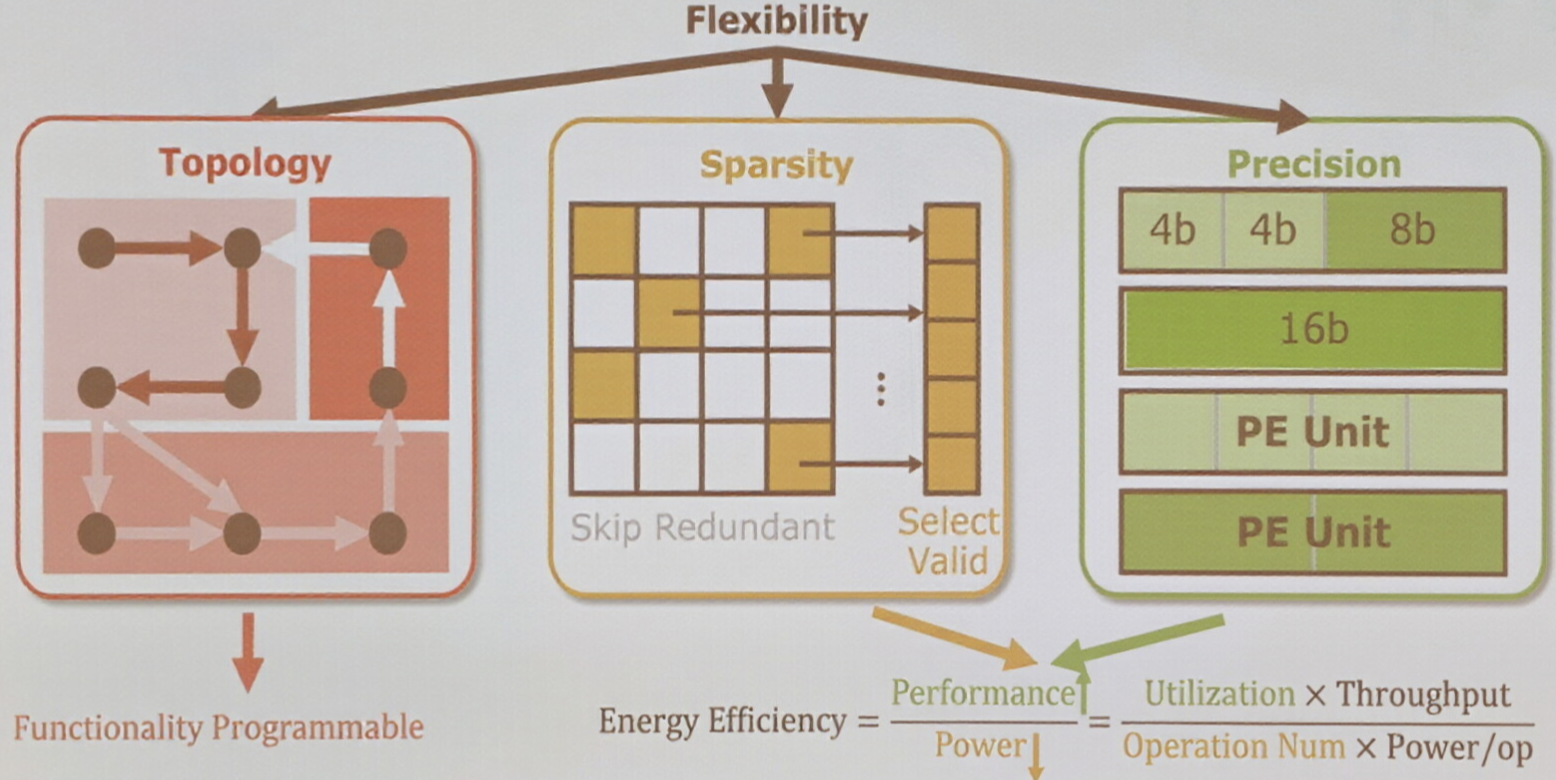
    alt text

总结

alt text
综上所述，面向 AI 的可重构处理器，其核心设计目标是实现是三个维度的“灵活性”

  • 适应不同拓扑的功能编程性
  • 跳过无效计算的稀疏性处理
  • 以及支持混合精度运算的可配置处理单元

这些灵活性的目的都是为了最大化一个核心指标：能效
能效由硬件利用率、吞吐量、实际有效操作数与功耗共同决定

软件编程 VS 硬件重构

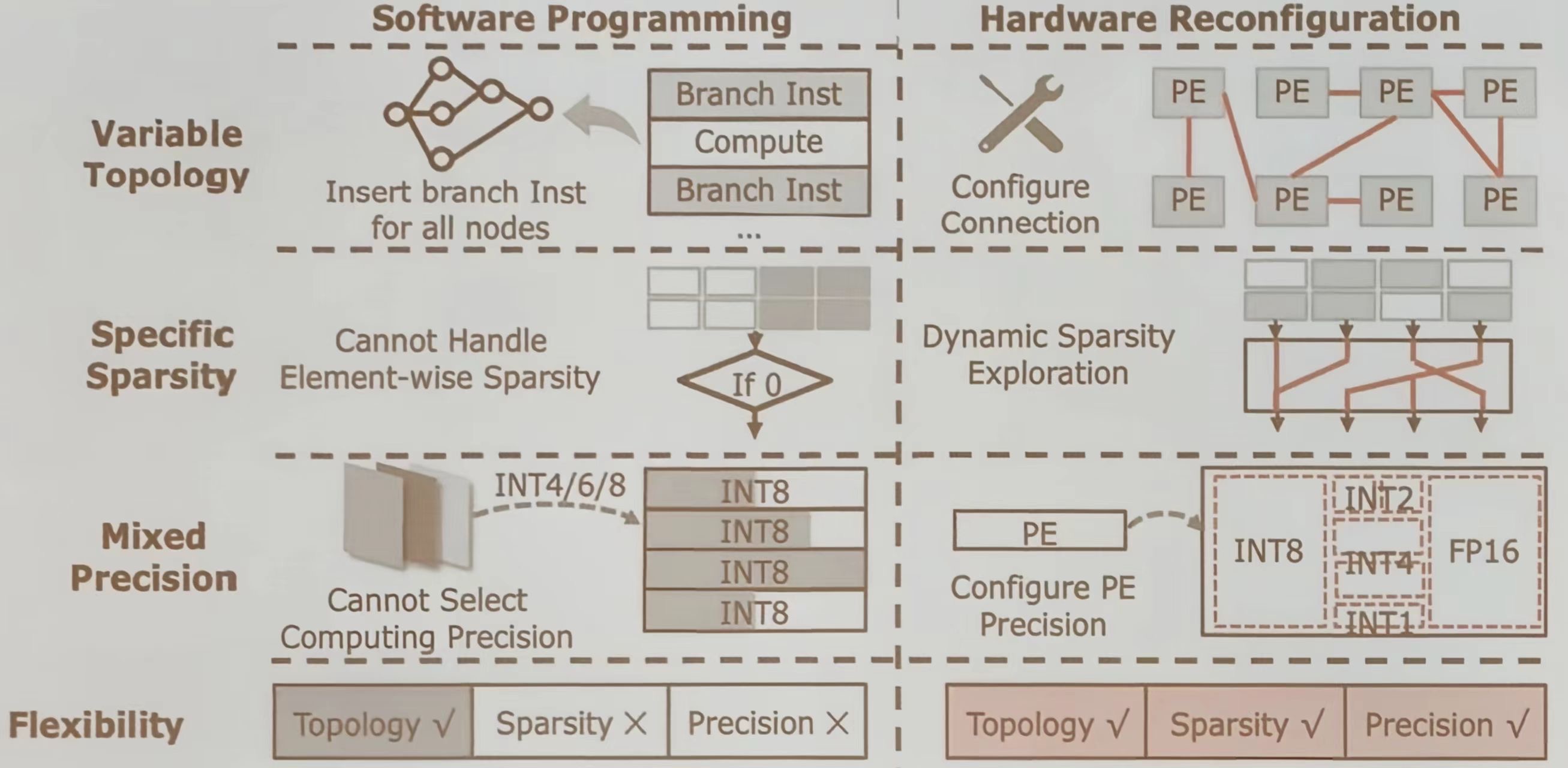
alt text

软件编程

  • 变量拓扑：通过插入分支指令来处理所有的节点，但这种方法在处理元素级稀疏性时存在局限
  • 特定稀疏性：无法有效处理元素级稀疏性
  • 混合精度：无法选择计算精度，通常固定为 INT 8

硬件重构

  • 变量拓扑：通过配置连接来实现，能够灵活应对不同的拓扑结构
  • 硬件重构：在拓扑、稀疏性和精度三个方面均具有较高的灵活性

重构抽象

为了实现上述的灵活性，我们可以将重构抽象为三个层次。

  • 芯片级重构关注全局，例如动态适应不同的稀疏模式以提升整体硬件利用率
  • 处理单元阵列（PEA）重构关注数据如何在处理单元（PE）流动，通过配置数据流来最大化数据复用
  • 处理单元级重构 (PE)则关注最基本的计算单元，通过位级别的重组来支持从低到高的不同运算精度。
    这三个层次共同构成了可重构 AI 处理器的设计框架

方法

PE-level 重构

让最基本的处理单元支持多样的数据精度。主要有三种技术路径：

  • 位串行方法在时间上逐位处理数据，功耗低但吞吐量也低
  • 位融合方法则在空间上组合多个低精度处理单元来形成更高精度的单元，能实现高吞吐量
  • 浮点融合方法，这对云端 AI 训练服务器至关重要
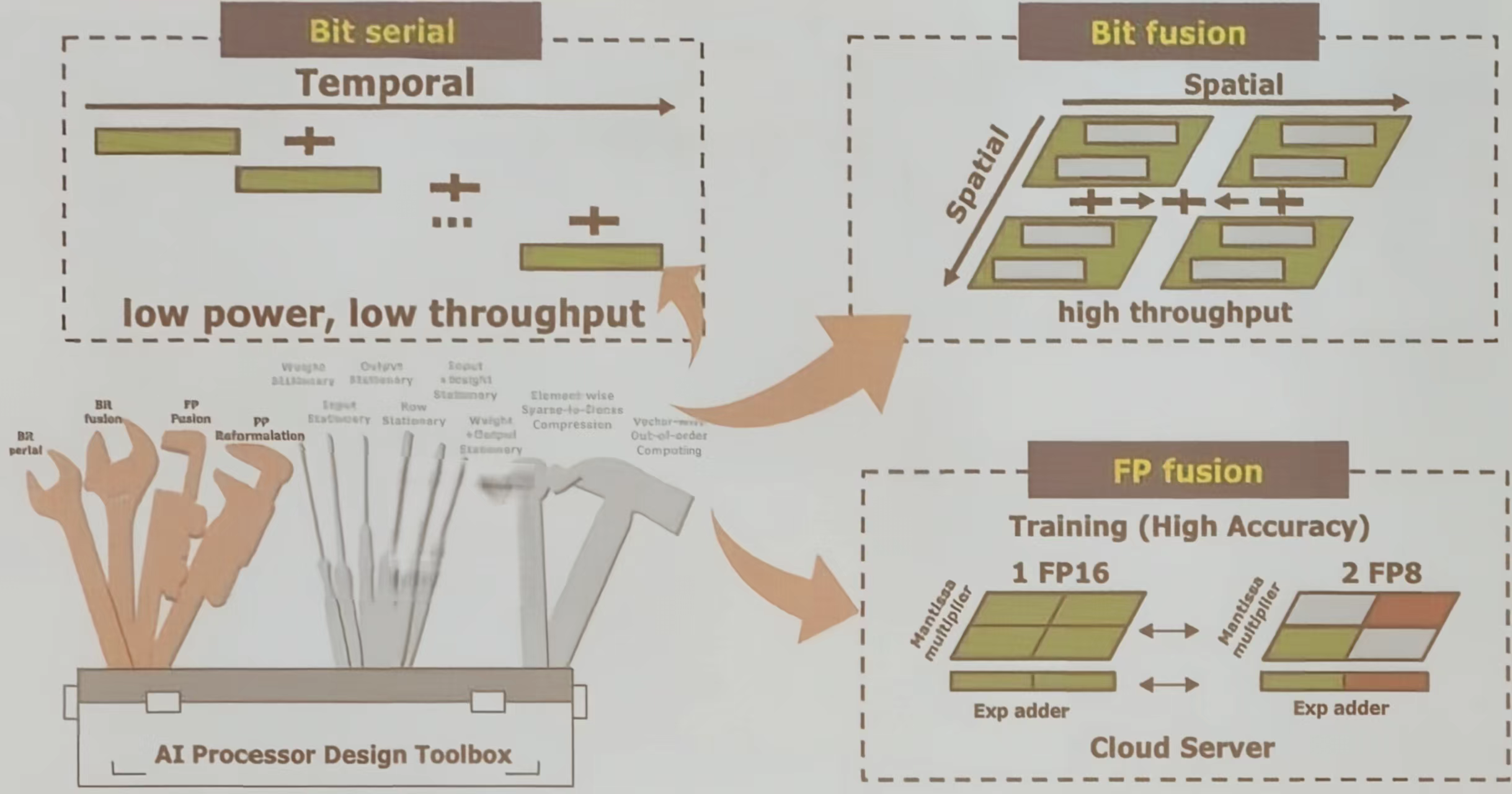
    alt text

位串行方法

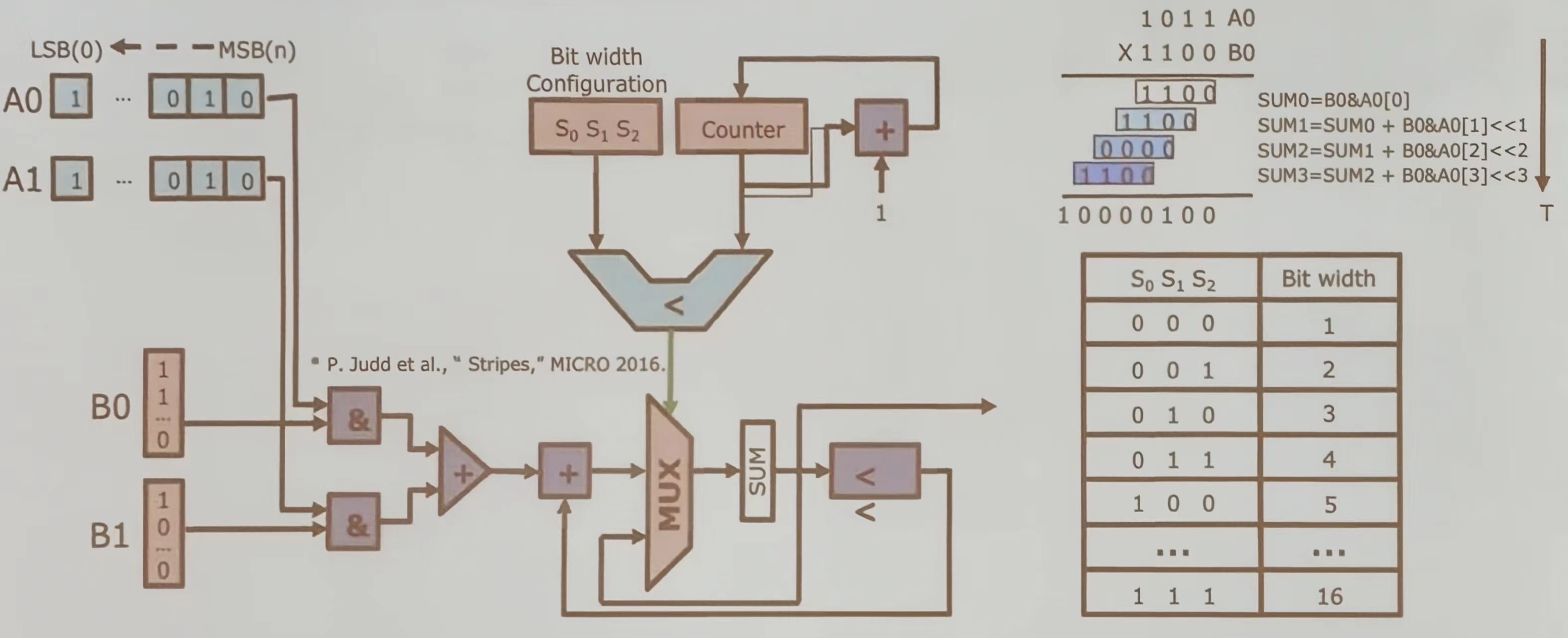
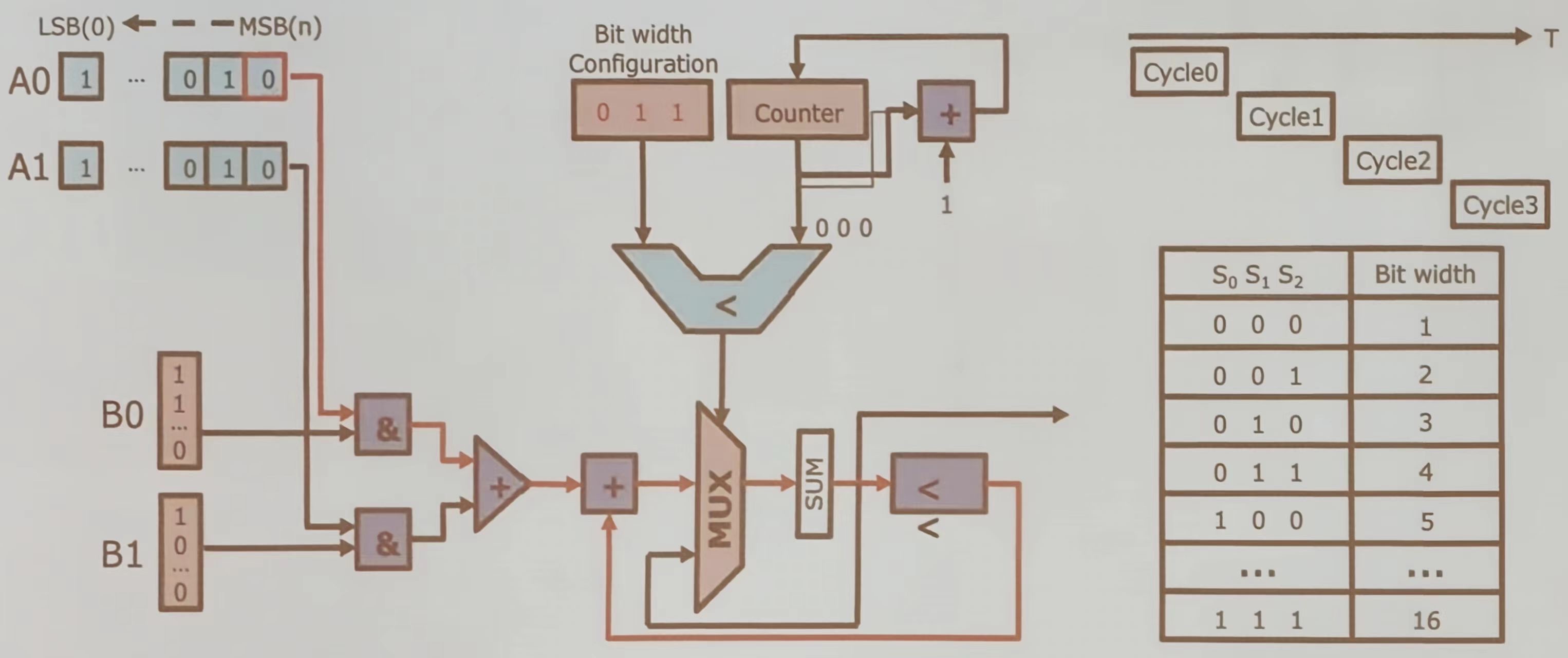
alt text
alt text

该设计主要用于动态调整数据处理的位宽，通过计数器和比较器控制多路选择器的选择，实现灵活的数据处理能力。

使用&门进行位与操作，生成部分积。使用加法器累加部分积，使用多路选择器根据当前位宽选择合适的部分积进行累加。最后再难过结果通过 SUM 模块输出，表示两个输入数的乘积。在每个周期内，电路处理一位输入数据，逐步累加部分积。根据 S 0, S 1, S 2 的值确定当前操作的位宽，从而控制循环次数。

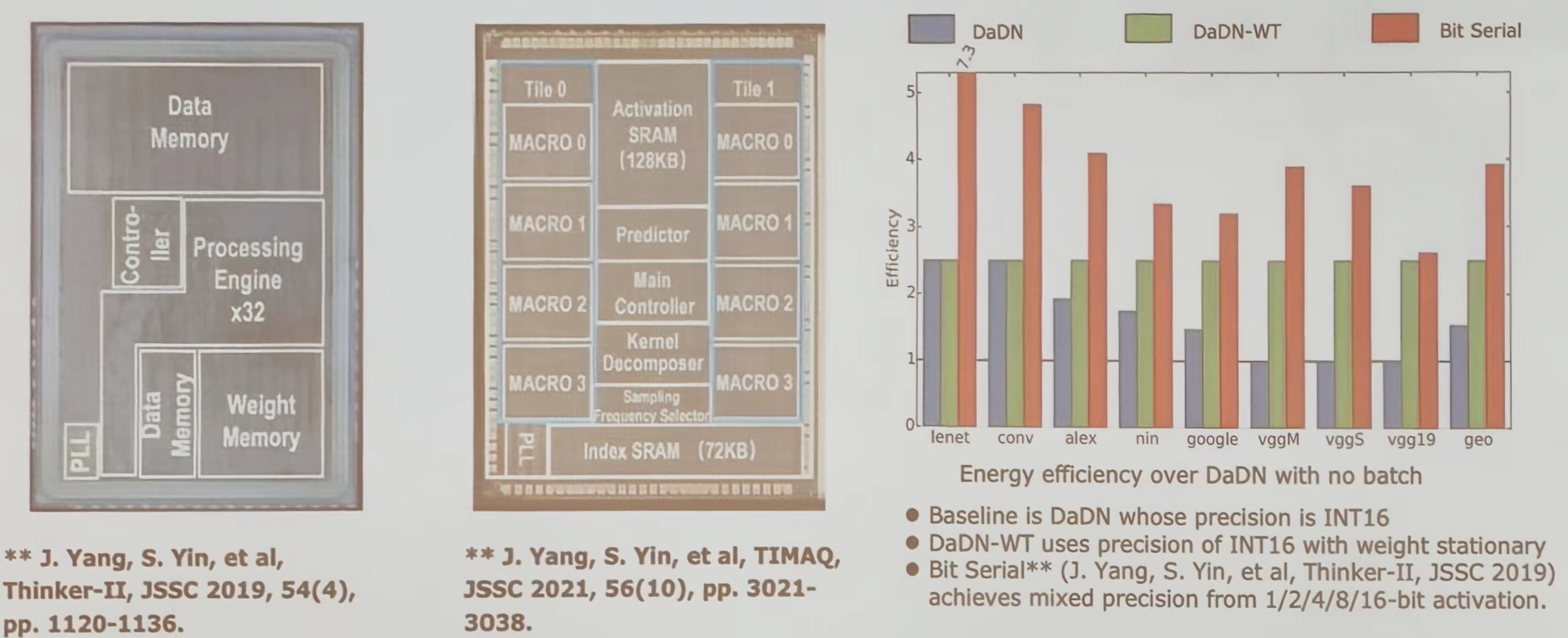
alt text

位融合方法

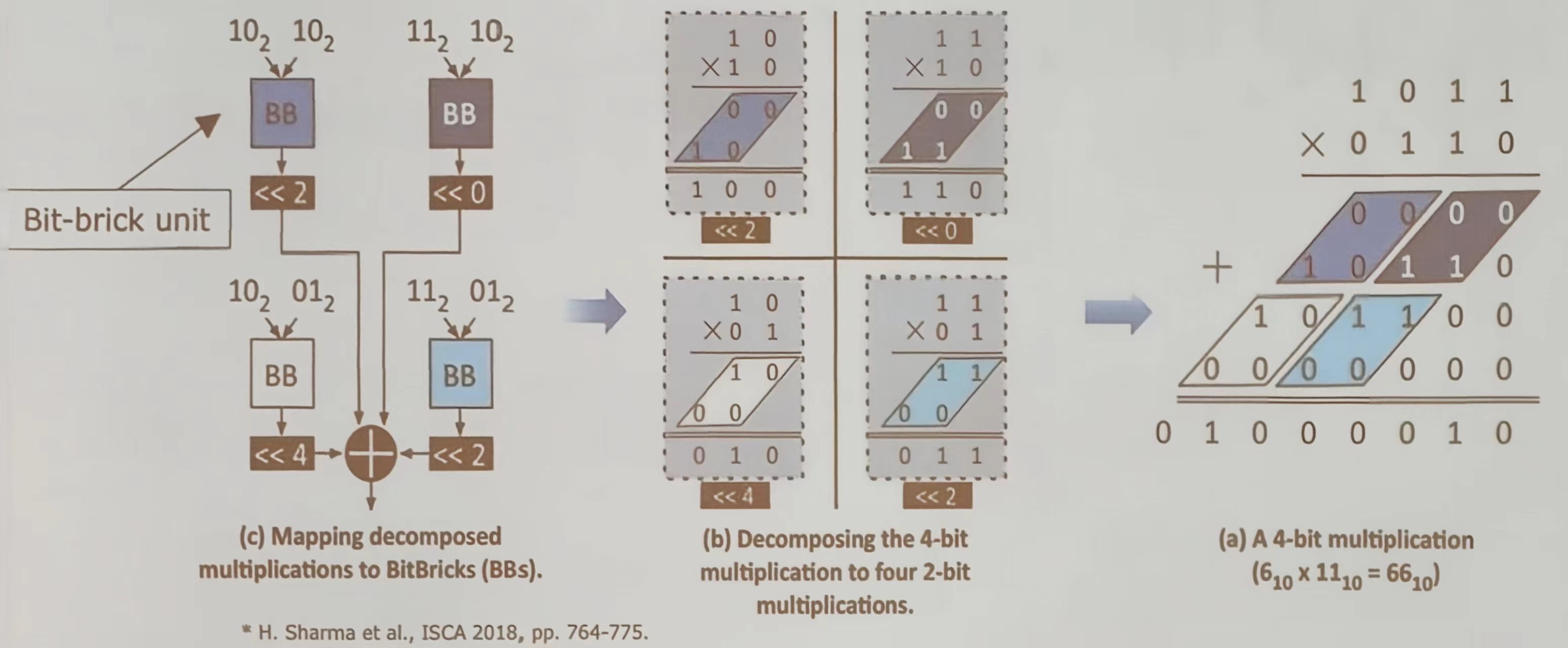
alt text

通过分解和映射的方式实现 4 位二进制的乘法运算。

  • 4 位乘法（a）：展示了两个 4 位二进制数（13 和 6）相乘的过程，结果为 78。通过逐位相乘和移位相加得到最终结果。
  • 分解为 4 个 2 位乘法（b）：将 4 位乘法分解为 4 个 2 位乘法操作。将每个 2 位乘法的结果通过移位（左移 2 位或 4 位）后相加，得到最终的乘积
  • 映射到 Bit-brick 单元 (c)：将分解后到 2 位乘法操作映射到 Bit-Brick (BB)。每个 Bit-Brick 单元执行一个 2 位乘法，并根据移位操作，最后将所有结果相加得到最终乘积
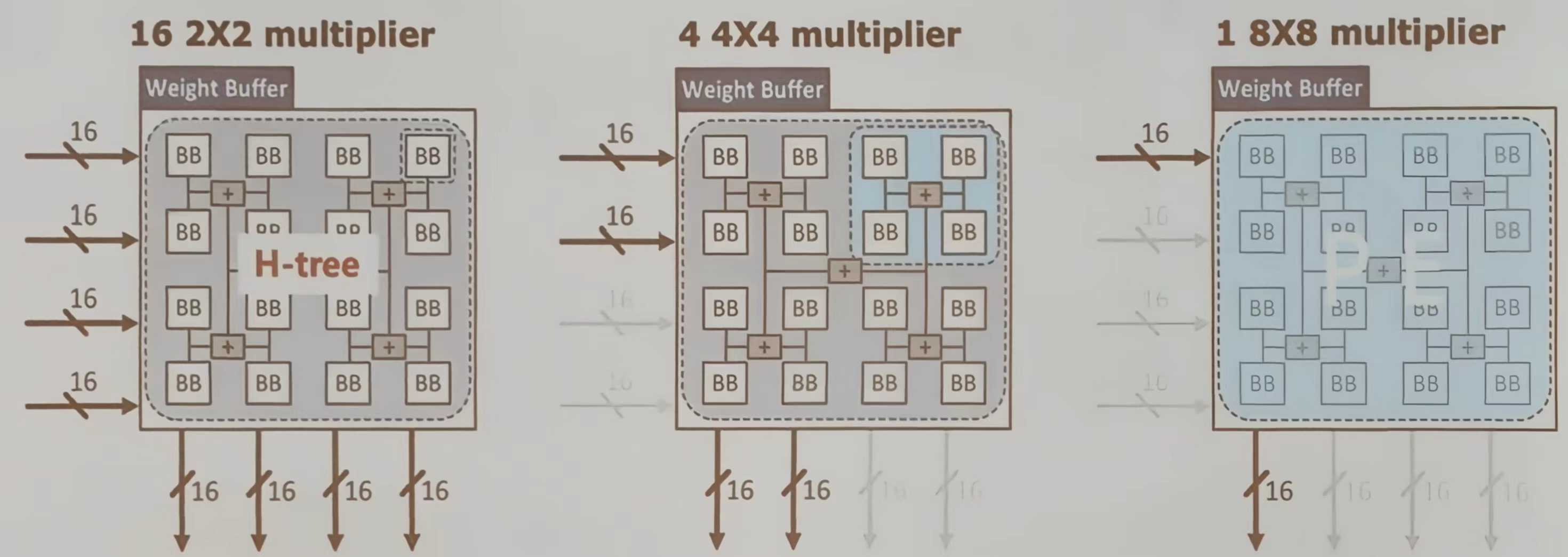
    alt text
    比如这三种不同的乘法器架构设计分别适用于不同规模的计算需求。选择合适的架构可以优化计算效率和资源利用率

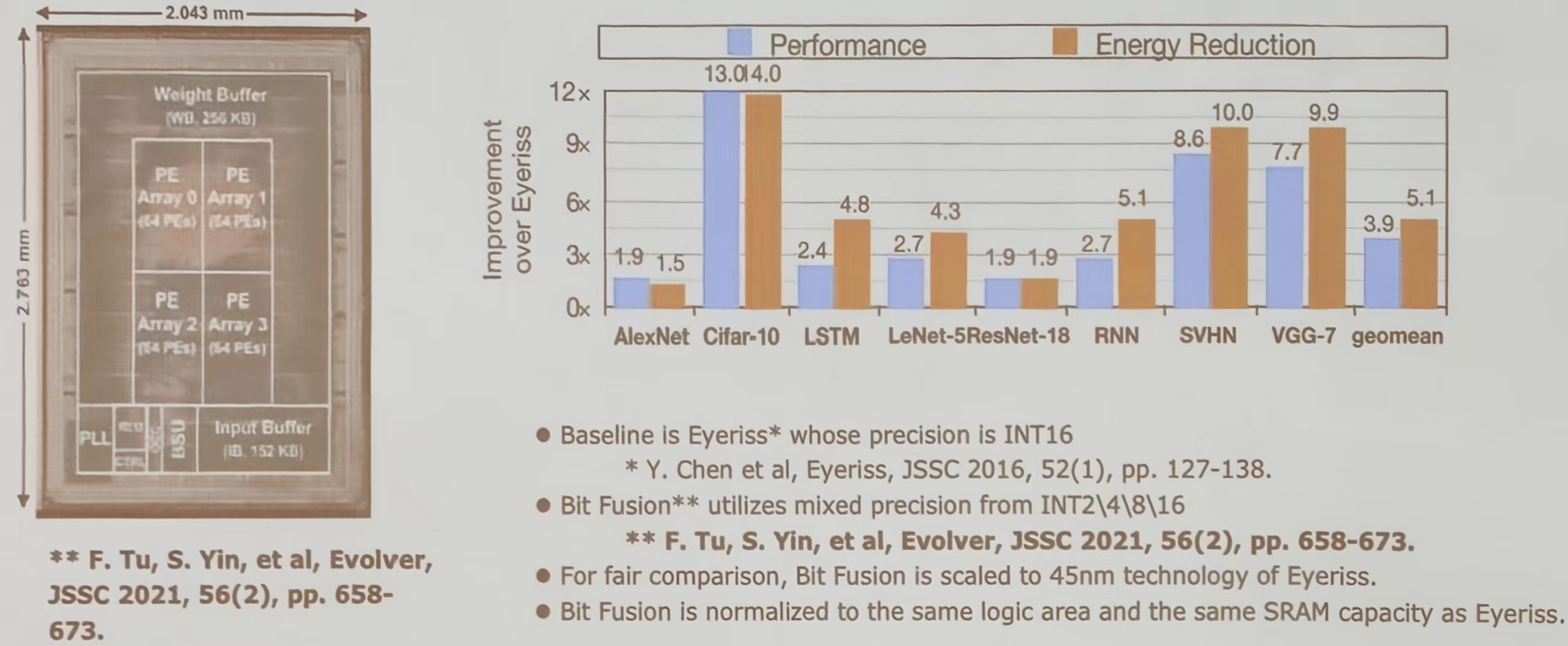
alt text

FP 融合方法

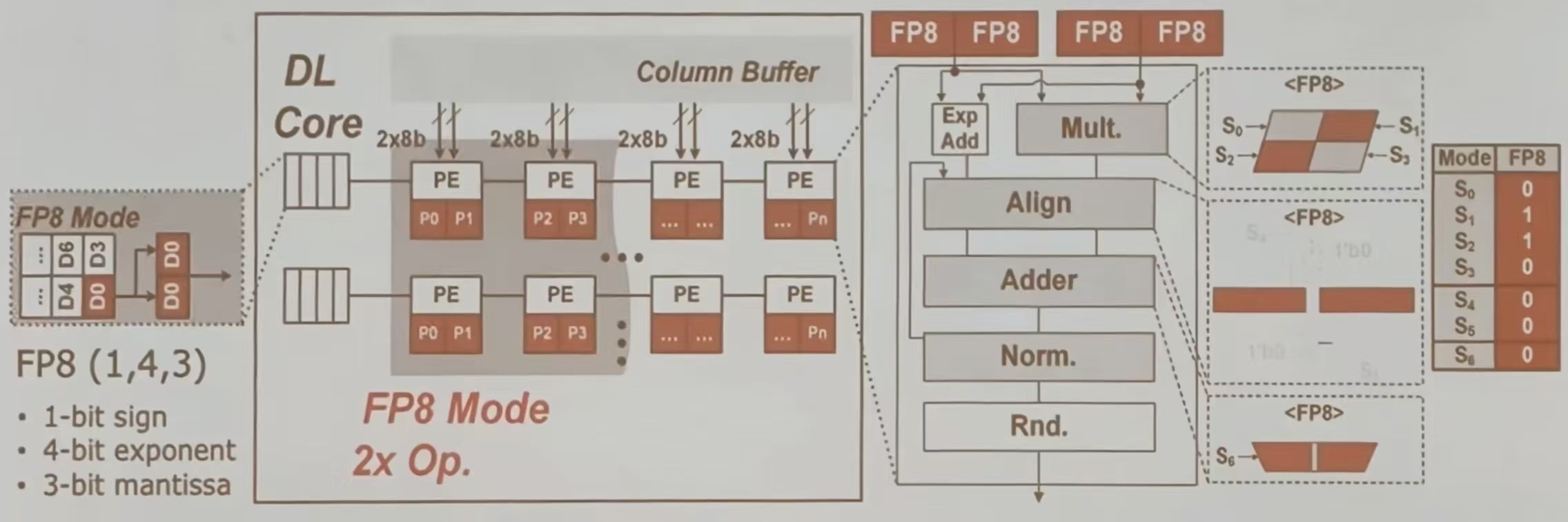
alt text
该图描述了在 PE 级重构中，如何通过共享逻辑实现 FP 8 模式下的高效计算。FP 8 模式利用 1 位符号、4 位指数和 3 位尾数的格式，在每个周期内完成 2 个 MAC 操作，从而提升计算效率。

在 DL Core 中包含多个处理单元 (PE)，每个 PE 都可以进行 2 x 8 b 的操作。Coloumn Buffer 用于存储和传输数据

在 FP 8 模式下，每个周期都可以执行 2 个 FP 8 MAC（乘加运算）操作。FP 单元共享乘法器、对齐器、加法器和归一化逻辑以实现重构。

FP 8 操作流程: 指数相加->乘法运算->对齐操作->加法运算->归一化->舍入

PEA-level 重构

面向最小数据访问的数据流重构

三种典型的数据流范式，分别对应于不同的数据复用策略

  • 输入静态：在 NxHxL 维度上保持输入数据不懂，适用于输入数据复用率高的场景
  • 输出静态：在 RxCxM 维度上保持输出数据不动，减少中间结果的移动
  • 权重静态；在 KxKxN 维度上保持权重数据不动，适用于权重复用率高的计算

两种 PEA（处理单元阵列）级重构方式：

  • 单体式重构：支持权重静态、输入静态、输出静态和行静态四种独立数据流模式
  • 交错式重构：可同时支持输入+权重静态、权重+输出静态等混合数据流模式
    这种灵活的数据流配置能力使得 AI 处理器能够更好地适配不同的神经网络结构的数据访问模式

可重构数据流-交错式重构

以生成对抗网络为例，说明在 GAN 等复杂模型中，生成器和判别器两种网络拓扑可能同时存在，对数据流提出不同要求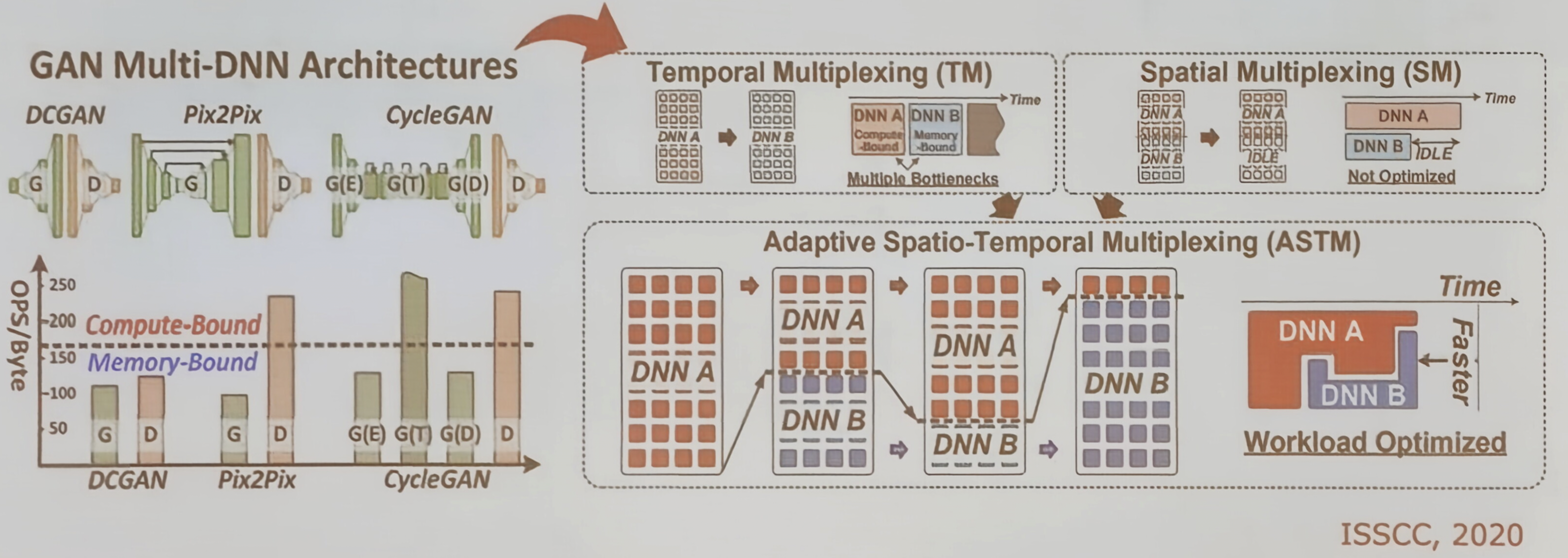
alt text

从输入照片到判别器输出“狗/猫”概率的过程，以及生成器与判别器之间的“极大极小博弈”

这种多拓扑共存的情况要求 AI 处理器具备在同一时间内处理不同数据流模式的能力。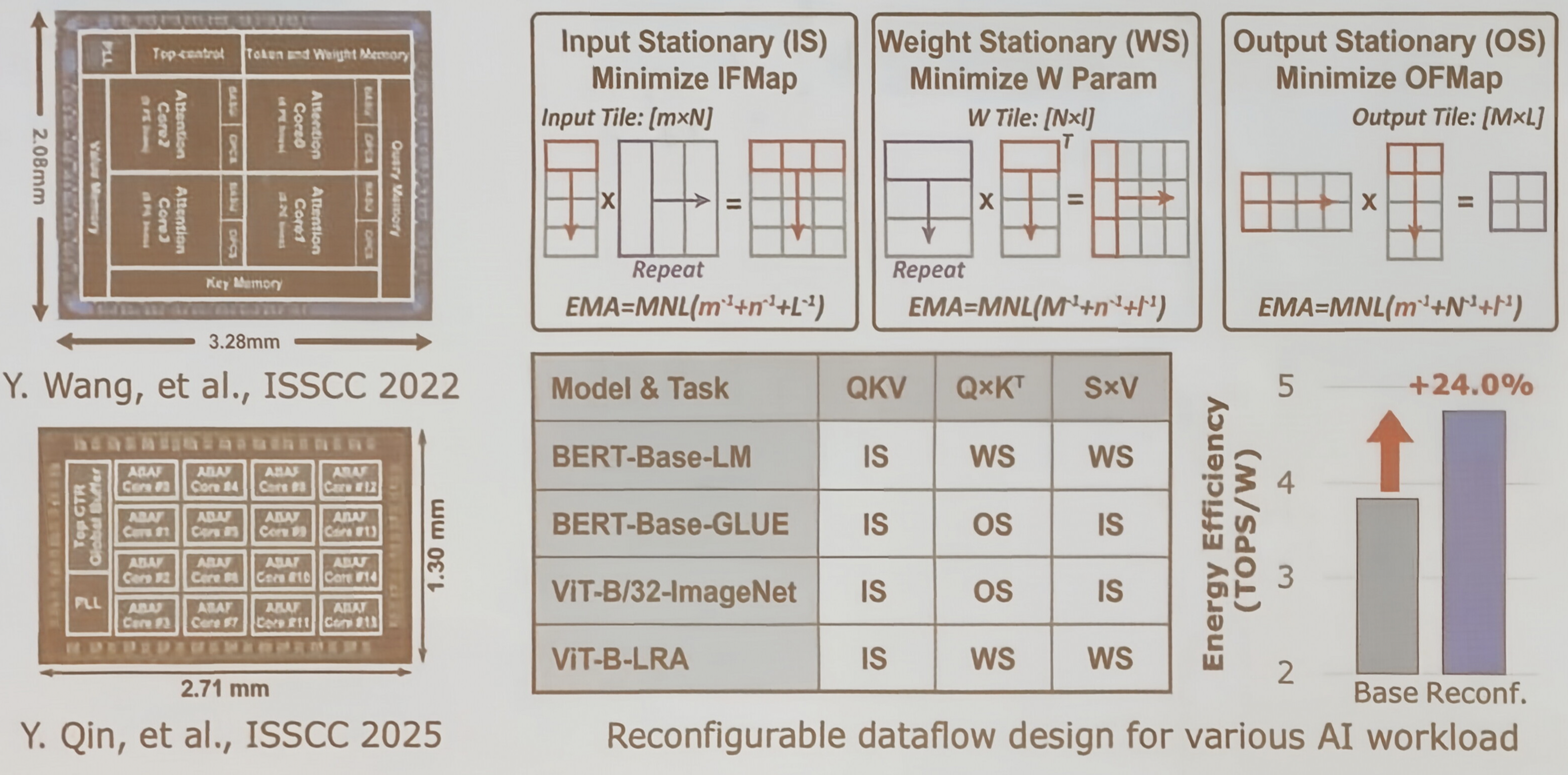
alt text
有三种多路复用策略来说明如何支持多神经网络拓扑：

  • 时分复用：在不同时间片执行不同 DNN
  • 空分复用：嫁给你硬件资源分区并行执行不同 DNN
  • 自适用时空复用：动态结合时分与空分，以最大硬件利用率。通过在 PEDA 级别实现混合数据流，可以有效地在同一硬件上灵活调度多种神经网络任务

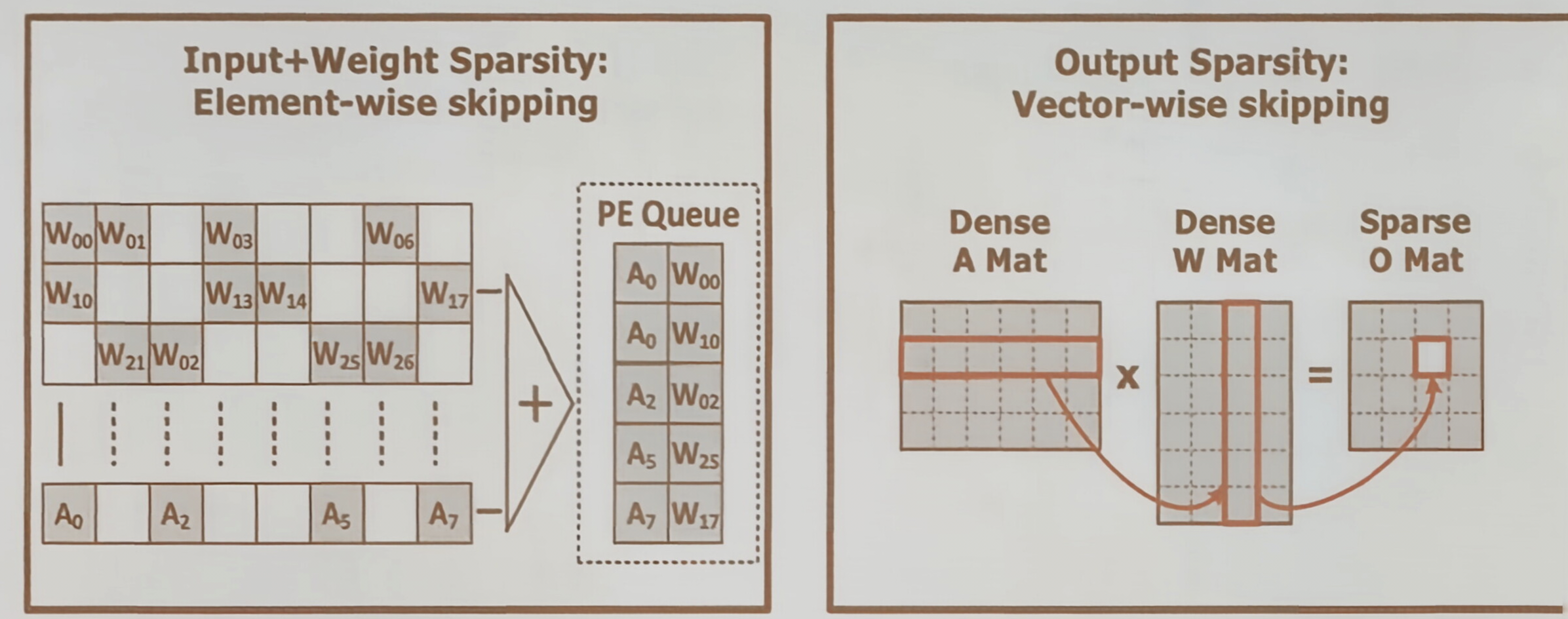
面向多种稀疏性的芯片级重构

该部分从三个层次介绍了如何通过芯片级重构来高效处理神经网络中的稀疏性：

  • 元素级：对稀疏矩阵进行压缩，仅计算非零元素
  • 向量级：支持乱序计算，跳过全零箱向量的运算
  • 向量间跳过：在向量点积中，若某一向量为零则跳过整个计算。
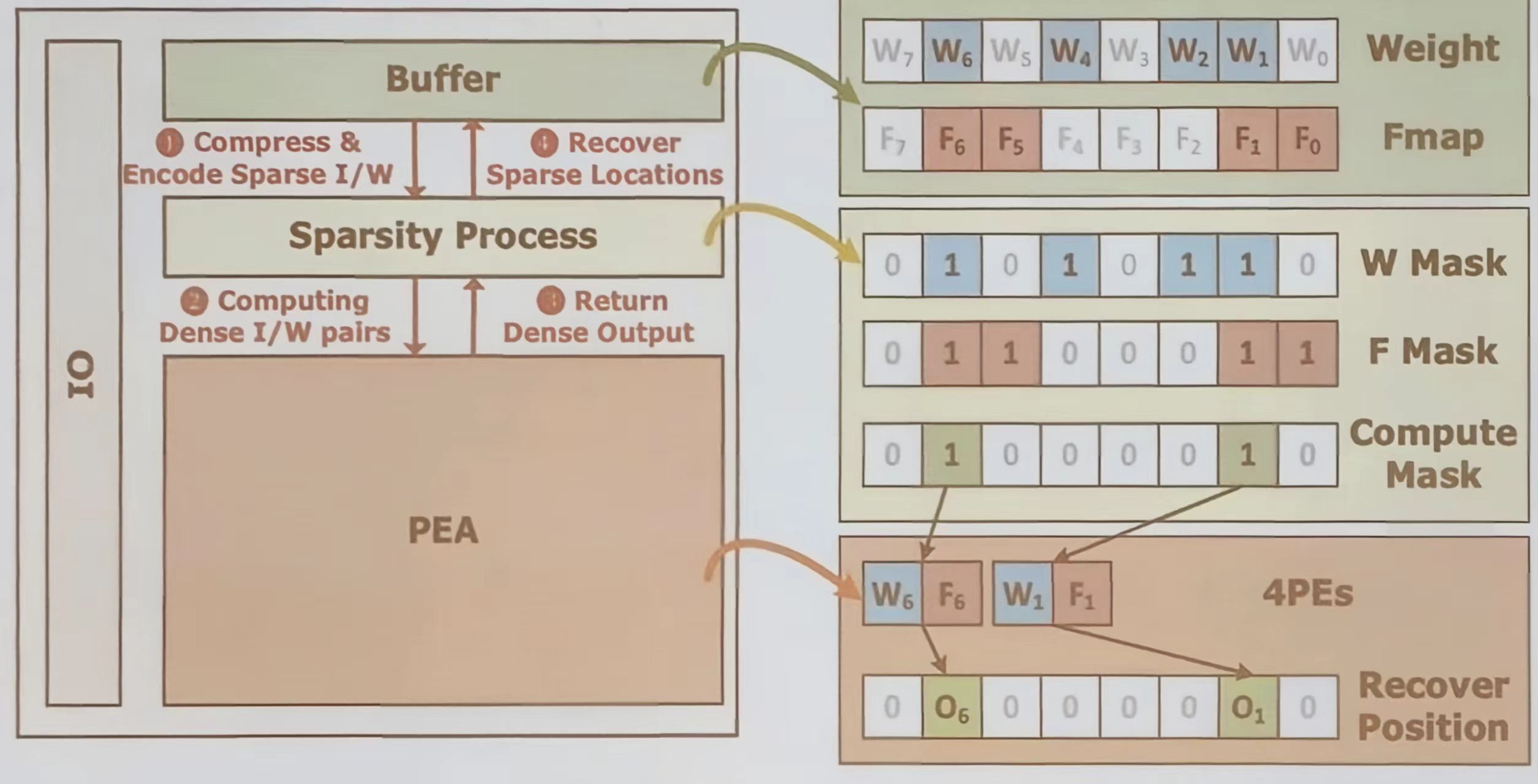
    alt text
    这些方法可以显著减少不必要的计算与数据移动
  • 在缓存中对稀疏的输入和权重进行压缩与编码
  • 生成计算掩码，仅对非零元素对执行计算
  • 在 PEA 中完成计算后，通过位置恢复逻辑重建输出的稠密格式。

BENES 网络

这是一种利用非对称 BENES 网络实现芯片级操作数路由的重构技术。

图示了一个 8 输入到 4 输出点 BENES 网络，它能够将 8 个输入到 4 个非零操作数动态路由到 4 个 PE 中进行计算。如果非零操作数超过 4 个，则将其拆分到两个周期完成。这种设计能够根据输入与权重的实时稀疏模式，灵活分配计算资源，最大化利用率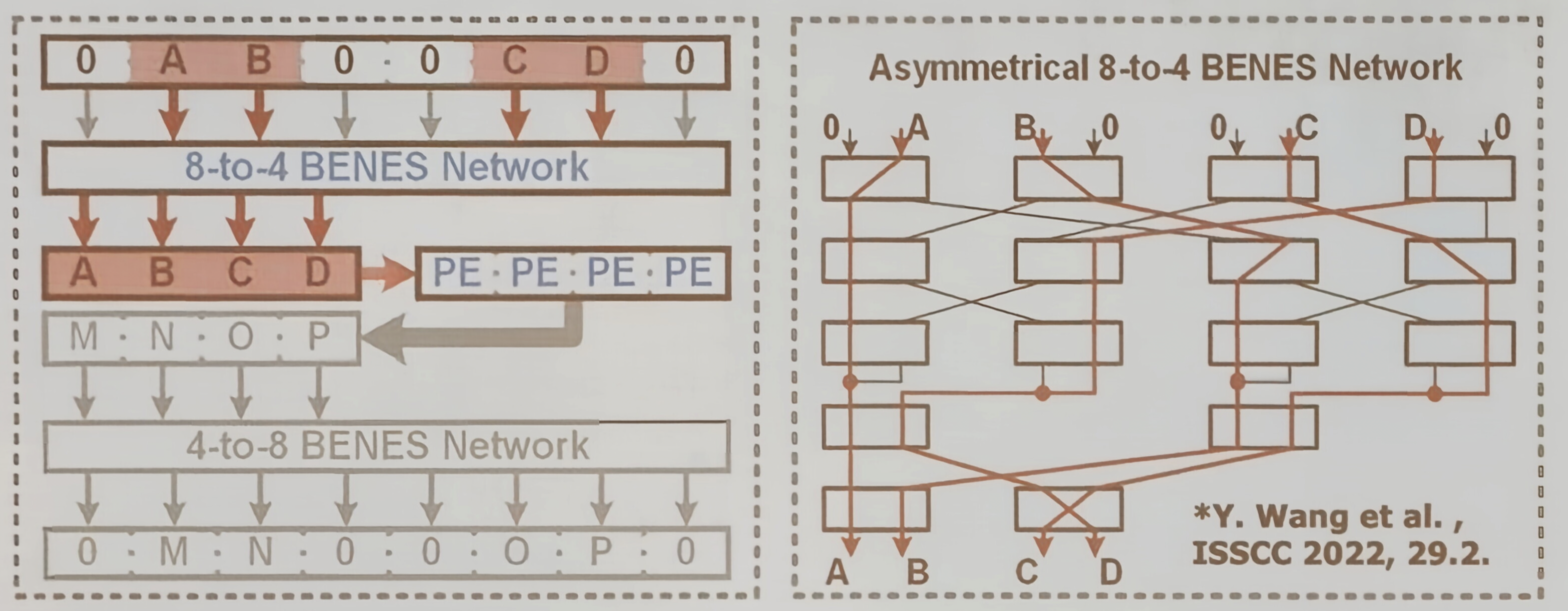
alt text

输入与权重稀疏性

通过一个简单数据流图示，说明当神经网络中输入和权重都具有稀疏性时，芯片级重构如何工作：稀疏的输入与权重相乘后产生输出，再经过 ReLU 激活函数可能进一步引入稀疏性。

输出稀疏性

即是输入和权重时稠密的，经过 Relu 等激活函数后，输出也可能变得稀疏。需要能能够识别并跳过对后续计算无贡献的零值输出，从而避免无效的数据移动与计算

总结

  • 芯片级重构：如 BENES 网络，处理操作数路由与稀疏计算
  • PEA 级重构：包括单体式与交错式数据流重构，适配不同网络拓扑
  • PE 级重构：涵盖位串行、位融合与浮点融合等技术，实现计算精度的灵活配置。

示例

重点介绍三家代表性企业的处理器：

  • SambaNova 的 RDA 处理器
  • Groq 张量流处理器
  • TsingMicro 的 RPU

SambaNova RDA 处理器

Kunle Olukotun 指出，数据流架构使计算能够围绕模型灵活组织，而非受限于固定指令流水线。

SambaNova 从硬件到软件均采用协同设计实现了从底层开始的可重构性。图中列出了其 SN-40 L 服务器的关键特性，如芯片级和 PEA 级重构、对稀疏计算的支持、多数据流处理能力及混合算子功能

Groq 张量流处理器

Groq 芯片的可重构性体现在两个层面：

  • 在 PEA 级，通过软件定义计算资源分配，并灵活配置水平和垂直的数据与指令流
  • 在芯片级，支持输出和权重的稀疏性处理，并能实现跨芯片的数据流协调

TsingMicro RPU

该产品线主要面向边缘计算场景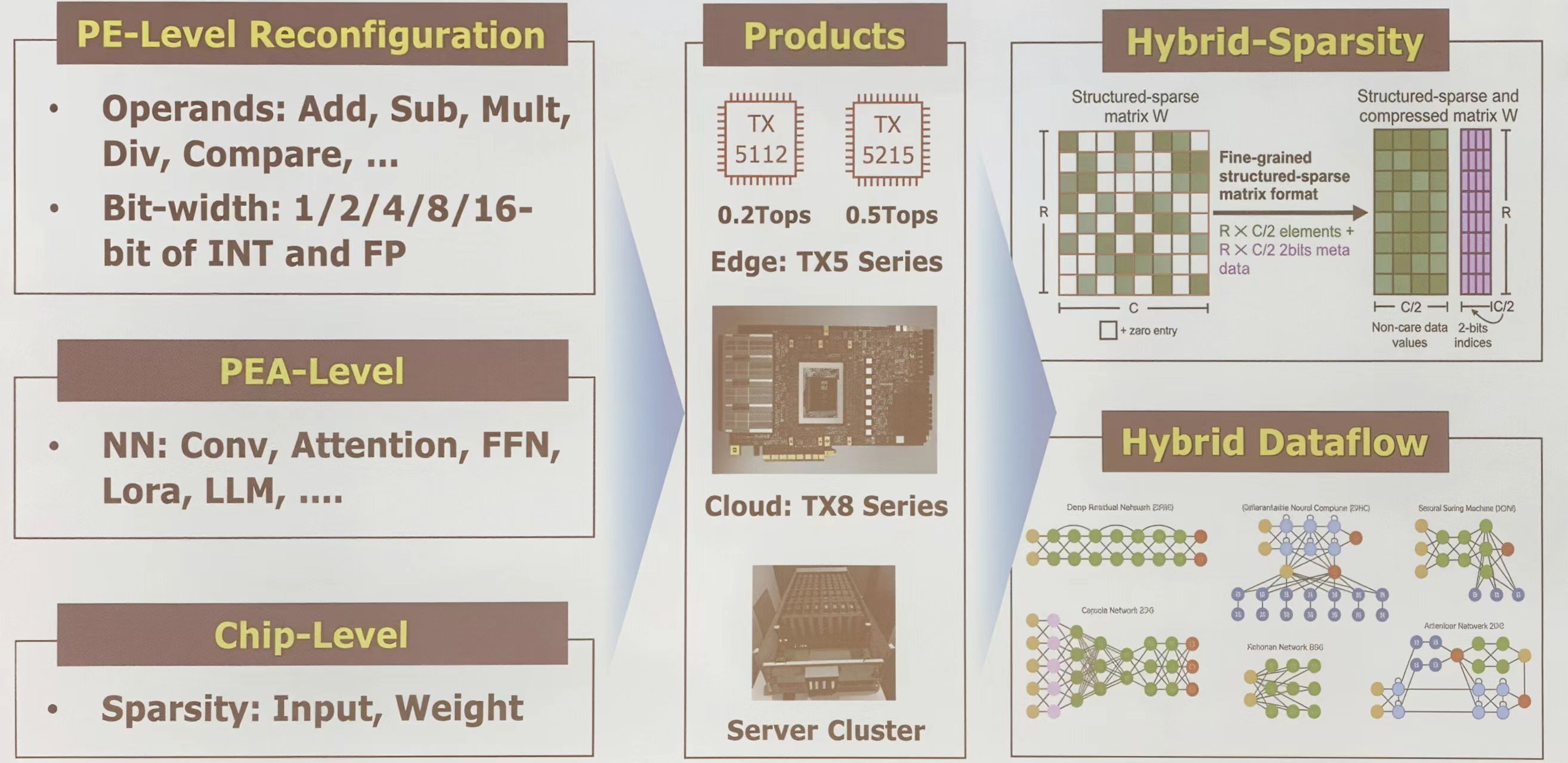
alt text

趋势

3 D 集成重构、多芯片重构、微观重构

结论

AI 模型的三大多样性特征：

  • 多样的网络拓扑
  • 多样的输入/权重/输出稀疏性
  • 推理/训练所需的不同数值精度

为了适配这些多样化的需求，硬件需要相应地在是那个层面进行重构

  • 在芯片级，进行稀疏处理重构，动态适应稀疏模式，提高处理单元利用率
  • 在 PEA 级，进行数据流重构，匹配不同神经网络拓扑，减少昂贵的内存访问
  • 在 PE 级，进行 MAC 运算单元重构，支持混合精度计算，从而最大化能效

参考资料

*PPT 及其图示来自 FPT 2025 讲座——可重构机器学习处理器：基本概念、应用与未来趋势（尹首一教授）